Unassigned Classes and Data Structures

Please assign this classes to one of the functionality groups of the CVR-Lib. More...

Functions
template<typename T >
void	cvr::householder (vector< T > &v, T &beta)
template<typename T >
void	cvr::householder (const vector< T > &src, vector< T > &v, T &beta)
template<typename T >
void	cvr::givens (const T &a, const T &b, T &c, T &s)

---

Detailed Description

Please assign this classes to one of the functionality groups of the CVR-Lib.

If your class does not fit into any of the current groups, please insert a new one in cvrlib/doc/src/cvrGroups.h

---

Function Documentation

template<typename T >

void cvr::givens	(	const T &	a,
		const T &	b,
		T &	c,
		T &	s
	)			[inline]

Calculates the cos (c) and sin (s) values needed for Givens Rotations.

The values c and s have the following property:

For more details see:
Gene H. Golub and Charles F. Van Loan, "Matrix Computations", 1996, The John Hopkins University Press, Baltimore and London

Parameters:

	a	first scalar
	b	second scalar
	c	cos value for Givens Rotation
	s	sin value for Givens Rotation

template<typename T >

void cvr::householder	(	const vector< T > &	src,
		vector< T > &	v,
		T &	beta
	)			[inline]

Calculates the Householder vector v and the factor beta for a vector src.

The resulting n-dimensional vector v has the following properties:

• v[0] = 1,
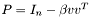• is orthogonal, and
• /f$ Px=||x||_2e_1 , where I_n is the n-by-n identity matrix and e_1 the first canonical vector.

Note: The on-place version of householder(vector<T>&, T&) is faster since the input vector is not copied first.

For more details see:
Gene H. Golub and Charles F. Van Loan, "Matrix Computations", 1996, The John Hopkins University Press, Baltimore and London

Parameters:

	src	vector x used to form the householder vector
	v	householder vector v
	beta	factor needed for householder transform

template<typename T >

void cvr::householder	(	vector< T > &	v,
		T &	beta
	)			[inline]

Calculates the Householder vector v and the factor beta for a vector x (given as input in v).

The resulting n-dimensional vector v has the following properties:

• v[0] = 1,
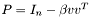• is orthogonal, and
• /f$ Px=||x||_2e_1 , where I_n is the n-by-n identity matrix and e_1 the first canonical vector.

For more details see:
Gene H. Golub and Charles F. Van Loan, "Matrix Computations", 1996, The John Hopkins University Press, Baltimore and London

Parameters:

	v	input: vector x; output: householder vector v
	beta	factor needed for householder transform