CVR-Lib last update 20 Sep 2009

Basic Math Functions
[Math]

Collaboration diagram for Basic Math Functions:

Functions

template<class T >
bool cvr::closeTo (const T &a, const T &b, const T epsilon=std::numeric_limits< T >::epsilon())
template<class T >
bool cvr::closeToZero (const T &a, const T epsilon=std::numeric_limits< T >::epsilon())
template<typename T >
T cvr::min (const T x, const T y)
template<typename T >
T cvr::max (const T x, const T y)
template<typename T >
T cvr::min (const T x, const T y, const T z)
template<typename T >
T cvr::max (const T x, const T y, const T z)
template<typename T >
T cvr::within (const T x, const T lower, const T upper)
template<typename T >
void cvr::minmax (const T x, const T y, T &theMin, T &theMax)
template<typename T >
void cvr::minmax (T &theMin, T &theMax)
template<typename T >
void cvr::minmax (const T x, T &theMin, T &theMax)
double cvr::degToRad (const double &deg)
float cvr::degToRad (const float &deg)
double cvr::degToRad (const int deg)
double cvr::radToDeg (const double &rad)
float cvr::radToDeg (const float &rad)
byte cvr::abs (byte x)
int cvr::abs (int x)
float cvr::abs (float x)
double cvr::abs (const double &x)
template<typename T >
T cvr::absdiff (const T &x, const T &y)
double cvr::reciprocal (const double &x)
float cvr::reciprocal (const float &x)
double cvr::oneMinus (const double &x)
float cvr::oneMinus (const float &x)
int cvr::oneMinus (const int x)
template<typename T >
T cvr::rectify (const T &x)
template<typename T >
T cvr::sqr (const T &x)
template<typename T >
T cvr::sqrAbs (const T &x)
int cvr::sqrt (int x)
unsigned int cvr::sqrt (unsigned int x)
float cvr::sqrt (const float &x)
double cvr::sqrt (const double &x)
template<typename T >
T cvr::sqrtrect (const T x)
float cvr::sigmoid (const float x)
double cvr::sigmoid (const double &x)
double cvr::sigmoid (const int x)
template<typename T >
T cvr::signum (T x)
template<typename T >
T cvr::signum0 (T x)
template<typename T >
bool cvr::even (const T x)
template<typename T >
bool cvr::odd (const T x)
template<typename T >
T cvr::round (T x)
template<typename T >
int cvr::iround (T x)
template<typename T >
long cvr::lround (T x)

Variables

const double cvr::Pi = 3.1415926535897932
const double cvr::NaN = log(-1.0)
const double cvr::Inf = tan(Pi/2.0)

Operators for complex numbers

template<typename T >
T cvr::sqrAbs (const complex< T > &x)

Function Documentation

double cvr::abs ( const double &  x  )  [inline]

Absolute value for any type.

float cvr::abs ( float  x  )  [inline]

Absolute value for any type.

int cvr::abs ( int  x  )  [inline]

Absolute value for integers.

byte cvr::abs ( byte  x  )  [inline]

Absolute value for signed bytes.

template<typename T >
T cvr::absdiff ( const T &  x,
const T &  y 
) [inline]

Absolute difference for the given values equals if (x>y) then (x-y) else (y-x).

Note that with complex numbers it does not return the real abs value.

template<class T >
bool cvr::closeTo ( const T &  a,
const T &  b,
const T  epsilon = std::numeric_limits<T>::epsilon() 
) [inline]

Returns true if a is close to b, i.e.

if abs(a-b) <= epsilon.

This is always better than testing equality with a==b for floating point types. For default epsilon integers are tested for equality.

Note: Do not used for unsigned types T.

Parameters:
a first value
b second value
epsilon max difference between a and b , default std::numeric_limits<T>::epsilon()
Returns:
true if distance between a and b is <= epsilon

template<class T >
bool cvr::closeToZero ( const T &  a,
const T  epsilon = std::numeric_limits<T>::epsilon() 
) [inline]

Returns true if a is close to T(0), i.e.

if abs(a) <= epsilon.

This is always better than testing equality with a==0. for floating point types. For default epsilon integers are tested for ==0 automagically.

Note: Do not used for unsigned types T.

Parameters:
a value
epsilon maximum absolute value of a , default std::numeric_limits<T>::epsilon()
Returns:
true if absolute value of a is <= epsilon

Referenced by cvr::arctanLUT::operator()().

double cvr::degToRad ( const int  deg  )  [inline]

Convert the given angle in degrees to an angle in radians.

float cvr::degToRad ( const float &  deg  )  [inline]

Convert the given angle in degrees to an angle in radians.

double cvr::degToRad ( const double &  deg  )  [inline]

Convert the given angle in degrees to an angle in radians.

template<typename T >
bool cvr::even ( const T  x  )  [inline]

Return true if the given number is an even number.

For floating point types, this function will return true only if the number is exacltly an integer and it is even.

template<typename T >
int cvr::iround ( T  x  )  [inline]

Round any float type mathematicly and return an integer.

Referenced by cvr::arctanLUT::operator()().

template<typename T >
long cvr::lround ( T  x  )  [inline]

Round any float type mathematicly and return an long integer.

template<typename T >
T cvr::max ( const T  x,
const T  y,
const T  z 
) [inline]

Get the maximum of x, y and z.

template<typename T >
T cvr::max ( const T  x,
const T  y 
) [inline]

Get the maximum of x and y.

template<typename T >
T cvr::min ( const T  x,
const T  y,
const T  z 
) [inline]

Get the minimum of x, y and z.

template<typename T >
T cvr::min ( const T  x,
const T  y 
) [inline]

Get the minimum of x and y.

template<typename T >
void cvr::minmax ( const T  x,
T &  theMin,
T &  theMax 
) [inline]

Store the minimum of x and theMin in theMin and the maximum of x and theMax in theMax, however, making just one comparison each time.

Warning:
This method assumes that theMin <= theMax, and if this condition is not met, be carefull as just one condition will be ensured, i.e. wether theMin will be ok or theMax, but not both.

template<typename T >
void cvr::minmax ( T &  theMin,
T &  theMax 
) [inline]

Ensure that the minimum of the two given values is stored in theMin and the maximum in theMax.

template<typename T >
void cvr::minmax ( const T  x,
const T  y,
T &  theMin,
T &  theMax 
) [inline]

Store the minimum of x and y in theMin and the maximum in theMax.

template<typename T >
bool cvr::odd ( const T  x  )  [inline]

Return true if the given number is an odd number.

For floating point types, this function will return true only if the number is exacltly an integer and it is odd.

int cvr::oneMinus ( const int  x  )  [inline]

Compute 1 minus the given value.

float cvr::oneMinus ( const float &  x  )  [inline]

Compute 1 minus the given value.

This function is usually employed to revert a probability value

double cvr::oneMinus ( const double &  x  )  [inline]

Compute 1 minus the given value.

This function is usually employed to revert a probability value

float cvr::radToDeg ( const float &  rad  )  [inline]

Convert the given angle in radians to an angle in degrees.

double cvr::radToDeg ( const double &  rad  )  [inline]

Convert the given angle in radians to an angle in degrees.

float cvr::reciprocal ( const float &  x  )  [inline]

Compute the reciprocal of the given value x, defined as 1/x.

double cvr::reciprocal ( const double &  x  )  [inline]

Compute the reciprocal of the given value x, defined as 1/x.

template<typename T >
T cvr::rectify ( const T &  x  )  [inline]

Rectify is 0 if x<0 or x otherwise.

template<typename T >
T cvr::round ( T  x  )  [inline]

Round any float type mathematicly.

double cvr::sigmoid ( const int  x  )  [inline]

Sigmoid for ints.

The sigmoid is defined as 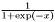$\frac{1}{1+\exp(-x)}$

double cvr::sigmoid ( const double &  x  )  [inline]

Sigmoid for doubles.

The sigmoid is defined as 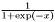$\frac{1}{1+\exp(-x)}$

float cvr::sigmoid ( const float  x  )  [inline]

Sigmoid for floats.

The sigmoid is defined as 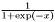$\frac{1}{1+\exp(-x)}$

template<typename T >
T cvr::signum ( T  x  )  [inline]

Signum of x (for x==0 -> signum = 1) (.

See also:
signum0)

template<typename T >
T cvr::signum0 ( T  x  )  [inline]

Signum of x (for x==0 -> signum = 0) (.

See also:
signum)

template<typename T >
T cvr::sqr ( const T &  x  )  [inline]

Square (x*x).

template<typename T >
T cvr::sqrAbs ( const T &  x  )  [inline]

Square of the magnitude of a number (|x|*|x|).

This function is useful in generic programming for those cases where complex numbers will occur in products of conjugate pairs.

template<typename T >
T cvr::sqrAbs ( const complex< T > &  x  )  [inline]

Square of the magnitude of a number (|x|*|x|).

This function is useful in generic programming for those cases where complex numbers will occur in products of conjugate pairs.

double cvr::sqrt ( const double &  x  )  [inline]

Square root.

float cvr::sqrt ( const float &  x  )  [inline]

Square root.

unsigned int cvr::sqrt ( unsigned int  x  )  [inline]

Square root.

int cvr::sqrt ( int  x  )  [inline]

Square root of integer type.

Equals floor(sqrt(x))

template<typename T >
T cvr::sqrtrect ( const T  x  )  [inline]

Square root of rectified value, i.e.

returns 0 if x<=0 or sqrt(x) otherwise.

template<typename T >
T cvr::within ( const T  x,
const T  lower,
const T  upper 
) [inline]

Check if the x value lies within the lower and upper bounds, and if not return the closest bound.

This is equivalent (but faster than) cvr::max(cvr::min(x,upper),lower).

Referenced by cvr::scale().

Variable Documentation

const double cvr::Inf = tan(Pi/2.0)

Constant Infinity (Inf) (double precision).

const double cvr::NaN = log(-1.0)

Constant Not a Number (NaN) (doble precision).

const double cvr::Pi = 3.1415926535897932

Constant Pi (double precision).

Generated on Sun Sep 20 22:08:34 2009 for CVR-Lib by Doxygen 1.5.8