cvr::quickMedian2 Class Reference
[Statistics]

Quick median for two vectors. More...

#include <cvrQuickMedian2.h>

Inheritance diagram for cvr::quickMedian2:

[legend]

Collaboration diagram for cvr::quickMedian2:

[legend]

List of all members.

Public Member Functions
	quickMedian2 ()
	quickMedian2 (const parameters &param)
	quickMedian2 (const eMedianEvenCase medianEvenCase)
	quickMedian2 (const quickMedian2 &other)
virtual	~quickMedian2 ()
const std::string &	name () const
virtual quickMedian2 *	clone () const
virtual quickMedian2 *	newInstance () const
const parameters &	getParameters () const
template<class V , class W >
bool	apply (V &keys, W &data, typename V::value_type &median) const
template<class V , class W >
bool	apply (V &keys, W &data) const
Protected Member Functions
template<class V , class W >
V::value_type	findMedian (V &vct, W &data, const int begin, const int end, const int medianPos) const
template<class V , class W >
int	partition (V &vct, W &data, const int begin, const int end) const

---

Detailed Description

Quick median for two vectors.

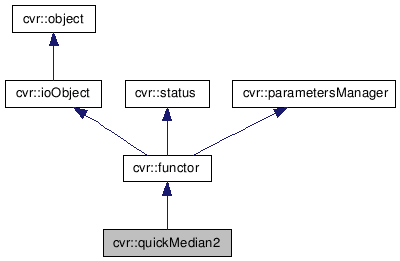
This class is used to extract the median of the elements of a given vector or matrix, partitioning at the same time a second vector. The median is defined as the element at the middle position of the sorted vector. The algorithm used is based on the quick sort.

The difference with the cvr::quickMedian functor is that you can "sort" a second vector, which might contain for example the indices of the elements. This way, you can easily find out, which elements of the original vector are under the median, and which ones above.

See also:

cvr::quickMedian, cvr::sort, cvr::sort2

For vectors (or matrices) with an even number n of elements, the median will be the element at (n/2) or (n/2)-1 depending on the parameter settings.

The type of the vector elements (T) must accept the operators < and >.

---

Constructor & Destructor Documentation

cvr::quickMedian2::quickMedian2

(

)

Default constructor.

cvr::quickMedian2::quickMedian2

(

const parameters &

param

)

Constructor to set parameters.

cvr::quickMedian2::quickMedian2

(

const eMedianEvenCase

medianEvenCase

)

Constructor with indicator what to do for even-sized vectors.

cvr::quickMedian2::quickMedian2

(

const quickMedian2 &

other

)

copy constructor

Parameters:

other

the object to be copied

virtual cvr::quickMedian2::~quickMedian2

(

)

[virtual]

Destructor.

---

Member Function Documentation

template<class V , class W >

bool cvr::quickMedian2::apply	(	V &	keys,
		W &	data
	)			const [inline]

Operates on the given arguments.

Please note that the arguments will be both modified.

The resulting keys vector contains the elements less or equal than the median for the indexes x such that x < size()/2, and higher or equal otherwise.

Both vectors must have the same size.

Parameters:

	keys	V with the key data. The median of this data is partially sorted while looking for the median.
	data	W with data to be sorted the same way as the keys. You can for example use a ivector initialized with the index values (i.e. data(i)=i), so that after the apply method you can check which elements are below the median and which above.

Returns:

bool upon success, false otherwise

template<class V , class W >

bool cvr::quickMedian2::apply	(	V &	keys,
		W &	data,
		typename V::value_type &	median
	)			const [inline]

Operates on the given arguments.

Please note that the arguments will be both modified.

The resulting keys vector contains the elements less or equal than the median for the indexes x such that x < size()/2, and higher or equal otherwise.

Both vectors must have the same size.

The types V and W, can be an cvr::genericVector or its derived classes, or a std::vector. In principle the container type V,W just needs to support:

• the type definitions V::size_type and V::value_type,
• the operator[] returning elements of type V::value_type
• the V::value_type has to be comparable with the operator<.
• the method empty()
• the method size() returning a V::size_type

Parameters:

	keys	vector with the key data. The median of this data is partially sorted while looking for the median.
	data	vector with data to be sorted the same way as the keys. You can for example use a ivector initialized with the index values (i.e. data(i)=i), so that after the apply method you can check which elements are below the median and which above.
	median	the median value of keys.

Returns:

bool upon success, false otherwise

virtual quickMedian2* cvr::quickMedian2::clone

(

)

const [virtual]

Returns a pointer to a clone of this functor.

Implements cvr::functor.

template<class V , class W >

V::value_type cvr::quickMedian2::findMedian	(	V &	vct,
		W &	data,
		const int	begin,
		const int	end,
		const int	medianPos
	)			const [inline, protected]

this method calculates the median in a recursively form

const parameters& cvr::quickMedian2::getParameters

(

)

const

Returns used parameters.

Reimplemented from cvr::parametersManager.

const std::string& cvr::quickMedian2::name

(

)

const [virtual]

Returns the name of this class.

Implements cvr::functor.

virtual quickMedian2* cvr::quickMedian2::newInstance

(

)

const [virtual]

Returns a pointer to a new instance of this functor.

Implements cvr::functor.

template<class V , class W >

int cvr::quickMedian2::partition	(	V &	vct,
		W &	data,
		const int	begin,
		const int	end
	)			const [inline, protected]

this method chooses a pivot-value and ensures that lower values lie at the left and higher values at the right of its final position, which will be returned.

---

The documentation for this class was generated from the following file:

• cvrQuickMedian2.h