cvr::svd Class Reference

Singular Value Decomposition (SVD). More...

#include <cvrSVD.h>

Inheritance diagram for cvr::svd:

[legend]

Collaboration diagram for cvr::svd:

[legend]

List of all members.

Classes
class	helper
	Helper class. More...
class	parameters
	The parameters for the class. More...
Public Member Functions
	svd ()
	svd (const parameters &params)
	svd (bool sort)
	svd (const svd &other)
virtual	~svd ()
virtual const std::string &	name () const
svd &	copy (const svd &other)
virtual svd *	clone () const
virtual svd *	newInstance () const
const parameters &	getParameters () const
bool	decomposition (fmatrix &src, fvector &w, fmatrix &v) const
bool	decomposition (dmatrix &src, dvector &w, dmatrix &v) const
virtual bool	apply (fmatrix &src, fvector &w, fmatrix &v) const
virtual bool	apply (dmatrix &src, dvector &w, dmatrix &v) const
virtual bool	apply (const fmatrix &src, fmatrix &u, fvector &w, fmatrix &v) const
virtual bool	apply (const dmatrix &src, dmatrix &u, dvector &w, dmatrix &v) const

---

Detailed Description

Singular Value Decomposition (SVD).

The functor will take a 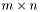matrix A and compute its singular value decomposition, consisting of three matrices U, W, and V, with

where 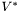denotes the conjugate transpose of V. U is a column-orthonormal 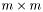matrix, W is a diagonal 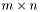matrix with the singular values on the diagonal, and V is a orthonormal 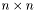matrix. Those columns of V whose corresponding entries in W are zero are the basis of A's null space.

You can find more theoretical information about a similar algorithm in W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery: Numerical Recipes in C, 2nd edition, Cambridge University Press, 1992. For a quick review check the Wikipedia at http://en.wikipedia.org/wiki/Singular_value_decomposition.

This class is usually employed in the computation of linear mean squared error. For a quick theory review check http://en.wikipedia.org/wiki/Linear_least_squares

Only instantiations of floating point types makes sense (i.e. for T double or float). If you want the singular values and corresponding singular vectors to be sorted, you have to set parameters::sort to true.

This class uses LAPACK if it is available.

See also:

singularValueDecomposition::parameters

---

Constructor & Destructor Documentation

cvr::svd::svd

(

)

Default constructor.

cvr::svd::svd

(

const parameters &

params

)

Default constructor with parameters.

cvr::svd::svd

(

bool

sort

)

Constructor.

Sets parameters::sort to the given value.

cvr::svd::svd

(

const svd &

other

)

Copy constructor.

virtual cvr::svd::~svd

(

)

[virtual]

Destructor.

---

Member Function Documentation

virtual bool cvr::svd::apply	(	const dmatrix &	src,
		dmatrix &	u,
		dvector &	w,
		dmatrix &	v
	)			const [virtual]

OnCopy version of Singular Value Decomposition.

Parameters:

	src	matrix<T> with the source matrix
	u	the U matrix
	w	vector<T> with the singular values, sorted descendingly if parameters::sort is true. The elements of this vector constitute the diagonal of the W matrix.
	v	the V matrix

Returns:

true is the decomposition was successfull, false if an error occured

virtual bool cvr::svd::apply	(	const fmatrix &	src,
		fmatrix &	u,
		fvector &	w,
		fmatrix &	v
	)			const [virtual]

OnCopy version of Singular Value Decomposition.

Parameters:

	src	matrix<T> with the source matrix
	u	the U matrix
	w	vector<T> with the singular values, sorted descendingly if parameters::sort is true. The elements of this vector constitute the diagonal of the W matrix.
	v	the V matrix

Returns:

true is the decomposition was successfull, false if an error occured

virtual bool cvr::svd::apply	(	dmatrix &	src,
		dvector &	w,
		dmatrix &	v
	)			const [virtual]

OnPlace version of Singular Value Decomposition.

Parameters:

	src	matrix<T> with the source matrix, will also contain the U matrix after the function has returned.
	w	vector<T> with the singular values, sorted descendingly if parameters::sort is true. The elements of this vector constitute the diagonal of the W matrix.
	v	the V matrix

Returns:

true is the decomposition was successfull, false if an error occured

virtual bool cvr::svd::apply	(	fmatrix &	src,
		fvector &	w,
		fmatrix &	v
	)			const [virtual]

OnPlace version of Singular Value Decomposition.

Parameters:

	src	matrix<T> with the source matrix, will also contain the U matrix after the function has returned.
	w	vector<T> with the singular values, sorted descendingly if parameters::sort is true. The elements of this vector constitute the diagonal of the W matrix.
	v	the V matrix

Returns:

true is the decomposition was successfull, false if an error occured

virtual svd* cvr::svd::clone

(

)

const [virtual]

Returns a pointer to a clone of this functor.

Implements cvr::functor.

svd& cvr::svd::copy

(

const svd &

other

)

Copy data of "other" functor.

Parameters:

other

the functor to be copied

Returns:

a reference to this functor object

bool cvr::svd::decomposition	(	dmatrix &	src,
		dvector &	w,
		dmatrix &	v
	)			const

OnPlace version of Singular Value Decomposition.

Singular Value Decomposition means that a m*n-matrix A is decomposed into three matrices U,W,V, such that A = U*W*V'. U is m*n, W is a diagonal matrix with n elements (which is implemented as vector), V is a n*n-matrix.

Note that the function returns V, not V'.

Parameters:

	src	matrix<T> with the source matrix, will also contain the U matrix after the function has returned. If src is a m*n matrix, U will also be of size m*n
	w	vector<T> with the singular values, sorted descendingly The elements of this vector constitute the diagonal of the W matrix.
	v	the V matrix

Returns:

true is the decomposition was successfull, false if an error occured

bool cvr::svd::decomposition	(	fmatrix &	src,
		fvector &	w,
		fmatrix &	v
	)			const

OnPlace version of Singular Value Decomposition.

Singular Value Decomposition means that a m*n-matrix A is decomposed into three matrices U,W,V, such that A = U*W*V'. U is m*n, W is a diagonal matrix with n elements (which is implemented as vector), V is a n*n-matrix.

Note that the function returns V, not V'.

Parameters:

	src	matrix<T> with the source matrix, will also contain the U matrix after the function has returned. If src is a m*n matrix, U will also be of size m*n
	w	vector<T> with the singular values, sorted descendingly The elements of this vector constitute the diagonal of the W matrix.
	v	the V matrix

Returns:

true is the decomposition was successfull, false if an error occured

const parameters& cvr::svd::getParameters

(

)

const

Returns used parameters.

Reimplemented from cvr::linearAlgebraFunctor.

virtual const std::string& cvr::svd::name

(

)

const [virtual]

Returns the name of this type ("svd").

Implements cvr::functor.

virtual svd* cvr::svd::newInstance

(

)

const [virtual]

Returns a pointer to a clone of this functor.

Implements cvr::functor.

---

The documentation for this class was generated from the following file:

• cvrSVD.h