CVR-Lib last update 20 Sep 2009

cvr::matrixTransform< I > Class Template Reference
[Geometric Image Transformations]

Class matrixTransform. More...

#include <cvrMatrixTransform.h>

Inheritance diagram for cvr::matrixTransform< I >:

Inheritance graph
[legend]
Collaboration diagram for cvr::matrixTransform< I >:

Collaboration graph
[legend]

List of all members.

Classes

class  helper2x2
 Helper for 2x2 matrix transformations. More...
class  helper2x3
 Helper for 2x3 matrix transformations. More...
class  helper3x3
 Helper for 2x3 matrix transformations. More...
class  helper4x3
 Helper for 4x3 matrix transformations. More...
class  helper4x4
 Helper for 4x4 matrix transformations. More...
class  helperBase
 Base class of helpers. More...
class  parameters
 The parameters for the class matrixTransform<T>. More...

Public Member Functions

 matrixTransform ()
 matrixTransform (const parameters &par)
 matrixTransform (const matrixTransform< I > &other)
virtual ~matrixTransform ()
virtual bool apply (matrix< value_type > &srcdest) const
virtual bool apply (const matrix< value_type > &src, matrix< value_type > &dest) const
virtual bool apply (matrix< value_type > &srcdest, fpoint &offset) const
virtual bool apply (const matrix< value_type > &src, matrix< value_type > &dest, fpoint &offset) const
matrixTransform & copy (const matrixTransform< I > &other)
matrixTransform & operator= (const matrixTransform< I > &other)
virtual const std::string & name () const
virtual matrixTransform< I > * clone () const
virtual matrixTransform< I > * newInstance () const
const parameters & getParameters () const
virtual bool updateParameters ()
bool setMatrix (const fmatrix &transMat)
Point transformation tools
The following tools permit to transform individual points, which is useful when looking for the direct and inverse transformations of particular pixels.

Before using any of this methods you MUST call the use() method first, in order for this class to know in what context it has to work, i.e., since the position of a pixel in the transformed matrix depends entirely on the dimension of the original image and the parameter settings, the use() method precomputes everything necessary to later transform each pixel more efficiently.

bool use (const ipoint &size)
void forwards (const fpoint &orig, fpoint &dest) const
void backwards (const fpoint &dest, fpoint &orig) const

Protected Member Functions

parameters & getParameters ()

Protected Attributes

helperBase * helper_
fpoint offset_
ipoint usedSize_

Detailed Description

template<class I>
class cvr::matrixTransform< I >

Class matrixTransform.

This is a template class, used to geometrically transform an image using a linear transformation expressed through a matrix.

Supported transformations.

The transformation matrix is provided in the parameters. It has to be invertible, and has to have a size of 2x2, 2x3, 3x3, 4x4 or 4x3.

Simple 2x2 transformation matrix

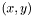The 2x2 transformation matrix transforms a pixel at $(x,y)$ into a pixel 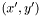$(x',y')$ with the following convention:

\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} m_{0,0} & m_{0,1} \\ m_{1,0} & m_{1,1} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} m_{0,0}x + m_{0,1}y \\ m_{1,0}x + m_{1,1}y \end{bmatrix} \]

It is usefull for rotation and scaling operations.

2x3 transformation matrix

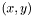The 2x3 transformation matrix uses homogeneous coordinates to transform a pixel at $(x,y)$ into a pixel 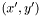$(x',y')$ with the following convention:

\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} m_{0,0} & m_{0,1} & m_{0,2}\\ m_{1,0} & m_{1,1} & m_{1,2} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} m_{0,0}x + m_{0,1}y + m_{0,2} \\ m_{1,0}x + m_{1,1}y + m_{1,2} \end{bmatrix} \]

It is usefull for rotation, scaling and translation operations.

3x3 transformation matrix

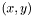The 3x3 transformation matrix uses homogeneous coordinates to transform a pixel at $(x,y)$ into a pixel 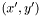$(x',y')$ with the following convention:

\[ \begin{bmatrix} x'' \\ y'' \\ \alpha \end{bmatrix} = \begin{bmatrix} m_{0,0} & m_{0,1} & m_{0,2}\\ m_{1,0} & m_{1,1} & m_{1,2}\\ m_{2,0} & m_{2,1} & m_{2,2} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} m_{0,0}x + m_{0,1}y + m_{0,2} \\ m_{1,0}x + m_{1,1}y + m_{1,2} \\ m_{2,0}x + m_{2,1}y + m_{2,2} \end{bmatrix} \]

The point 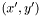$(x',y')$ is obtained with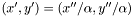 $(x',y') = (x''/\alpha,y''/\alpha)$

It can be used for rotation, scaling and translation operations, but using the third line, more interesting mappings can be achieved.

3x4 transformation matrix

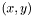The 3x4 transformation matrix uses homogeneous coordinates to transform a pixel at $(x,y)$ into a pixel 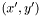$(x',y')$ with the following convention:

\[ \begin{bmatrix} x'' \\ y'' \\ \alpha \end{bmatrix} = \begin{bmatrix} m_{0,0} & m_{0,1} & m_{0,2} & m_{0,3}\\ m_{1,0} & m_{1,1} & m_{1,2} & m_{1,3}\\ m_{2,0} & m_{2,1} & m_{2,2} & m_{2,3} \end{bmatrix} \begin{bmatrix} x \\ y \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} m_{0,0}x + m_{0,1}y + m_{0,3} \\ m_{1,0}x + m_{1,1}y + m_{1,3} \\ m_{2,0}x + m_{2,1}y + m_{2,3} \end{bmatrix} \]

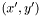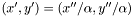The point $(x',y')$ is obtained with $(x',y') = (x''/\alpha,y''/\alpha)$.

It can be used for rotation, scaling and translation operations, but using the third line, more interesting mappings can be achieved.

Please note that this configuration is in principle equivalent to a 3x3 matrix, as the third column is "absorved" by the z=0 assumption for the pixel positions on the image plane.

4x4 transformation matrix

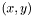The 4x4 transformation matrix uses homogeneous coordinates to transform a pixel at $(x,y)$ into a pixel 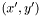$(x',y')$ with the following convention:

\[ \begin{bmatrix} x'' \\ y'' \\ z'' \\ \alpha \end{bmatrix} = \begin{bmatrix} m_{0,0} & m_{0,1} & m_{0,2} & m_{0,3}\\ m_{1,0} & m_{1,1} & m_{1,2} & m_{1,3}\\ m_{2,0} & m_{2,1} & m_{2,2} & m_{2,3}\\ m_{3,0} & m_{3,1} & m_{3,2} & m_{3,3} \end{bmatrix} \begin{bmatrix} x \\ y \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} m_{0,0}x + m_{0,1}y + m_{0,3} \\ m_{1,0}x + m_{1,1}y + m_{1,3} \\ m_{2,0}x + m_{2,1}y + m_{2,3} \\ m_{3,0}x + m_{3,1}y + m_{3,3} \\ \end{bmatrix} \]

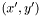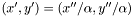The point $(x',y')$ is obtained with $(x',y') = (x''/\alpha,y''/\alpha)$.

It can be used for rotation, scaling and translation operations, but using the z coordinates, more interesting mappings can be achieved, like perspective projections.

4x3 transformation matrix

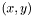The 4x3 transformation matrix uses homogeneous coordinates to transform a pixel at $(x,y)$ into a pixel 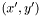$(x',y')$ with the following convention:

\[ \begin{bmatrix} x'' \\ y'' \\ z'' \\ \alpha \end{bmatrix} = \begin{bmatrix} m_{0,0} & m_{0,1} & m_{0,2}\\ m_{1,0} & m_{1,1} & m_{1,2}\\ m_{2,0} & m_{2,1} & m_{2,2}\\ m_{3,0} & m_{3,1} & m_{3,2} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} m_{0,0}x + m_{0,1}y + m_{0,2} \\ m_{1,0}x + m_{1,1}y + m_{1,2} \\ m_{2,0}x + m_{2,1}y + m_{2,2} \\ m_{3,0}x + m_{3,1}y + m_{3,2} \\ \end{bmatrix} \]

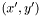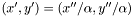The point $(x',y')$ is obtained with $(x',y') = (x''/\alpha,y''/\alpha)$.

It can be used for rotation, scaling and translation operations, but using the z coordinates, more interesting mappings can be achieved, like perspective projections.

Example

The following example rotates an image on the axis parallel to the y axis but passing through the middle of the image.

   // type definitions just for shorter names.
   typedef cvr::nearestNeighborInterpolation<cvr::rgbaPixel> inter_type;
   typedef cvr::matrixTransform< inter_type > trans_type;
   trans_type transformer;

   // get an image to work with
   cvr::ioImage loader;
   cvr::viewer2D view("Image");
   cvr::image img,img2;
   if (!loader.load("../img/testImg.bmp",img)) {
     std::cout << loader.getStatusString() << std::endl;
     exit(1);
   }

   cvr::fmatrix mat,pro;

   // generate a projection matrix to give a perspective effect
   pro = cvr::projection(1000.0f);

   cvr::ipoint o = img.size()/2;

   // animation of 360 images rotated.
   for (int deg=0;deg<=360;++deg) {
     float rad=degToRad(static_cast<float>(deg)); // angle in radians

     // generate a transformation matrix using several elemental operations
     mat =
       cvr::translation(fpoint3D(o.x,o.y,0)) *
       pro *
       cvr::rotation(fpoint3D(0.0f,0.0f,0.0f),fpoint3D(1,0,0),rad) *
       cvr::translation(fpoint3D(-o.x,-o.y,0));

       transformer.setMatrix(mat);
       transformer.apply(img,img2);

       view.show(img2);
   }

Template parameter

The template parameter I indicates the interpolator type to be used. The class provided must be inherited from cvr::fixedGridInterpolation. Note that the interpolator works for one type of containers only, and only that type will be supported by this class too.

See also:
matrixTransform<I>::parameters.

Constructor & Destructor Documentation

template<class I>
cvr::matrixTransform< I >::matrixTransform (  ) 

Default constructor.

template<class I>
cvr::matrixTransform< I >::matrixTransform ( const parameters &  par  ) 

Construct a functor using the given parameters.

template<class I>
cvr::matrixTransform< I >::matrixTransform ( const matrixTransform< I > &  other  ) 

Copy constructor.

Parameters:
other the object to be copied

template<class I>
virtual cvr::matrixTransform< I >::~matrixTransform (  )  [virtual]

Destructor.

Member Function Documentation

template<class I>
virtual bool cvr::matrixTransform< I >::apply ( const matrix< value_type > &  src,
matrix< value_type > &  dest,
fpoint &  offset 
) const [virtual]

Transform geometrically the source image and leave the result on the destination container.

If the parameters specify to AdjustDimensions, then the offset value will contain the relative position of the dest origin with respect to the original image coordinate system. To all other resize policies, the value of offset is set to (0,0).

If you need to find out where in the rotated image is located the origin of the initial image, then that would be in -offset.

Parameters:
src matrix<value_type> with the source data.
dest matrix<value_type> where the result will be left.
offset position of the origin of the result with respect to the coordinate system of the original image.
Returns:
true if apply successful or false otherwise.

Implements cvr::geometricTransform< I >.

template<class I>
virtual bool cvr::matrixTransform< I >::apply ( matrix< value_type > &  srcdest,
fpoint &  offset 
) const [virtual]

Transform geometrically the given image and leave the result on the same container.

If the parameters specify to AdjustDimensions, then the offset value will contain the relative position of the srcdest origin with respect to the original image coordinate system. To all other resize policies, the value of offset is set to (0,0).

If you need to find out where in the rotated image is located the origin of the initial image, then that would be in -offset.

Parameters:
srcdest matrix<T> with the source data. The result will be left here too.
offset position of the origin of the result with respect to the coordinate system of the original image.
Returns:
true if apply successful or false otherwise.

Reimplemented from cvr::geometricTransform< I >.

template<class I>
virtual bool cvr::matrixTransform< I >::apply ( const matrix< value_type > &  src,
matrix< value_type > &  dest 
) const [virtual]

Transform geometrically the source image and leave the result on the destination container.

Operates on a copy of the given parameters.

Parameters:
src matrix<value_type> with the source data.
dest matrix<value_type> where the result will be left.
Returns:
true if apply successful or false otherwise.

Implements cvr::geometricTransform< I >.

template<class I>
virtual bool cvr::matrixTransform< I >::apply ( matrix< value_type > &  srcdest  )  const [virtual]

Transform geometrically the given image and leave the result on the same container.

Parameters:
srcdest matrix<T> with the source data. The result will be left here too.
Returns:
true if apply successful or false otherwise.

Reimplemented from cvr::geometricTransform< I >.

template<class I>
void cvr::matrixTransform< I >::backwards ( const fpoint &  dest,
fpoint &  orig 
) const

Inverse transform the given point coordinates.

Warning:
Do not forget to provide first the size of the matrix from which the points are going to be taken, using use(const ipoint&).
This method is the inverse of forwards(const fpoint&,fpoint&). Given a position dest in the transformed system, it computes the coordinates of that point in the original coordinate system.

Parameters:
dest Position of a point in the transformed space.
orig Position of the point in the original space.

template<class I>
virtual matrixTransform<I>* cvr::matrixTransform< I >::clone (  )  const [virtual]

Returns a pointer to a clone of this functor.

Implements cvr::geometricTransform< I >.

template<class I>
matrixTransform& cvr::matrixTransform< I >::copy ( const matrixTransform< I > &  other  ) 

Copy data of "other" functor.

Parameters:
other the functor to be copied
Returns:
a reference to this functor object

template<class I>
void cvr::matrixTransform< I >::forwards ( const fpoint &  orig,
fpoint &  dest 
) const

Transform the given point coordinates.

Warning:
Do not forget to provide first the size of the matrix from which the points are going to be taken, using use(const ipoint&).
This method takes the orig position, assumed to be in a reference system of a matrix/image of the size given by the use(const ipoint&) method, and transforms this position according to the set parameters.

template<class I>
parameters& cvr::matrixTransform< I >::getParameters (  )  [protected]

Returns used parameters.

Reimplemented from cvr::geometricTransform< I >.

template<class I>
const parameters& cvr::matrixTransform< I >::getParameters (  )  const

Returns used parameters.

Reimplemented from cvr::geometricTransform< I >.

template<class I>
virtual const std::string& cvr::matrixTransform< I >::name (  )  const [virtual]

Returns the complete name of the functor class.

Reimplemented from cvr::geometricTransform< I >.

template<class I>
virtual matrixTransform<I>* cvr::matrixTransform< I >::newInstance (  )  const [virtual]

Returns a pointer to a new instance of this functor.

Implements cvr::geometricTransform< I >.

template<class I>
matrixTransform& cvr::matrixTransform< I >::operator= ( const matrixTransform< I > &  other  ) 

Alias for copy member.

Parameters:
other the functor to be copied
Returns:
a reference to this functor object

template<class I>
bool cvr::matrixTransform< I >::setMatrix ( const fmatrix &  transMat  ) 

Shortcut for setting the transformation matrix without changing the rest of the parameters.

The matrix has to have valid dimensions: 2x2, 2x3, 3x3, 4x4 or 4x3.

template<class I>
virtual bool cvr::matrixTransform< I >::updateParameters (  )  [virtual]

Update functor state on a parameters change.

Reimplemented from cvr::geometricTransform< I >.

template<class I>
bool cvr::matrixTransform< I >::use ( const ipoint &  size  ) 

Provide the size of the matrix from which it will be assumed the positions will be taken.

Parameters:
size Size of the matrix from which the positions will be analyzed
Returns:
true if everything is ok, or false if the matrix set in the parameters is not invertible or some other weird problem.

Member Data Documentation

template<class I>
helperBase* cvr::matrixTransform< I >::helper_ [protected]

Pointer to the actual helper being used.

This pointer is managed by the updateParameters() method.

template<class I>
fpoint cvr::matrixTransform< I >::offset_ [protected]

Last offset computed in use();.

template<class I>
ipoint cvr::matrixTransform< I >::usedSize_ [protected]

Last size indicated with use().

The documentation for this class was generated from the following file:
Generated on Sun Sep 20 22:08:49 2009 for CVR-Lib by Doxygen 1.5.8